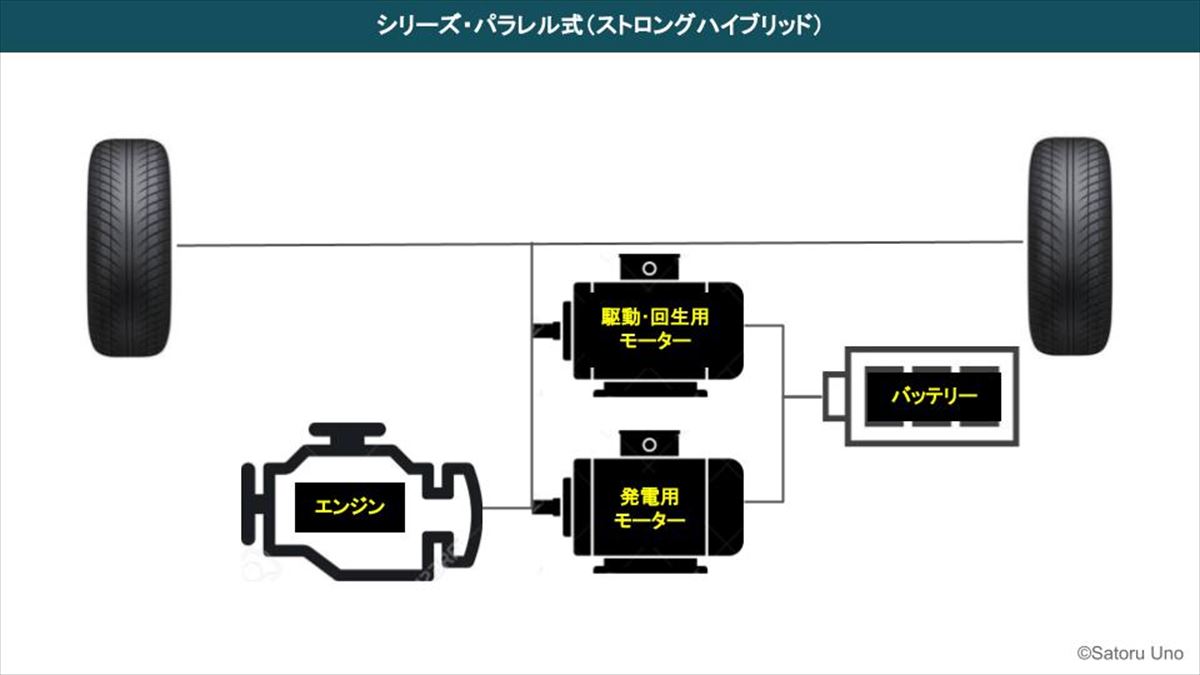
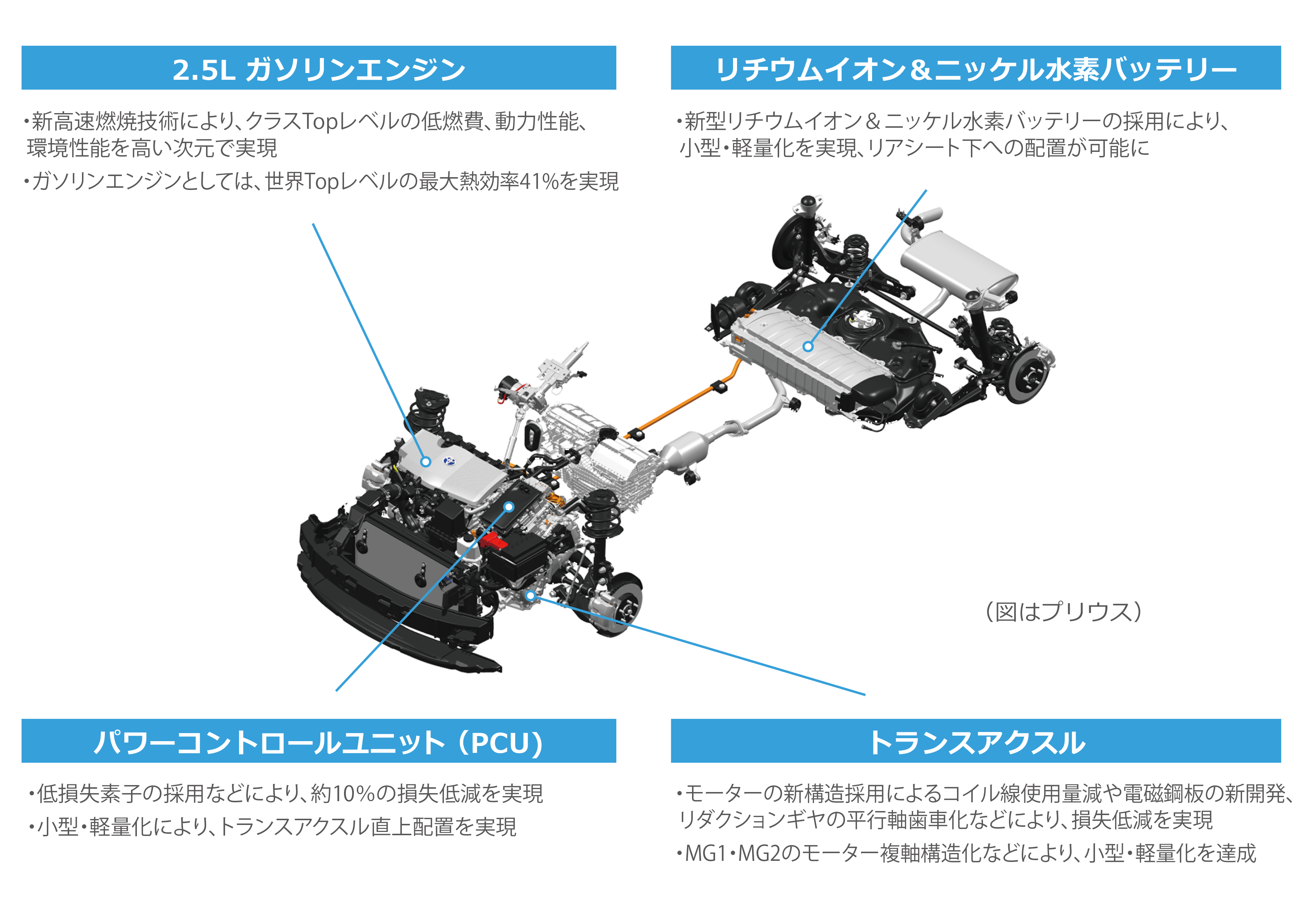
ハイブリッドシステム(英: hybrid system)は、連続的な挙動と離散的な挙動が混在する動的システムである。 形式的には、連続的な振舞いを記述する常微分方程式や差分方程式に離散事象システムを組み合わせることによって記述される。 他の用法との混同を避けるため、ハイブリッドダイナミカルシステム (hybrid dynamical system; HDS) とも呼ばれる。
ハイブリッドシステムでは連続的および離散的な挙動を統一的に扱うことが出来るため、伝統的な動的システムに基づいた制御理論と比べて広範な制御対象へと適用することが可能である。 その概念は古くから知られていたが、計算機科学における離散事象システムの研究の発展を契機にシステム制御分野での関心が高まり、近年急速に発展を遂げている。
一般的なシステムモデル
ハイブリッドシステムの一般的なモデルは次のように記述される。
ただし、 と はそれぞれ時刻 におけるシステムの連続状態 (continuous state) および 離散状態 (discrete state) である。離散状態はモード (mode) とも呼ばれる。連続および離散状態の組 をハイブリッド状態 (hybrid state)、あるいは単に状態と呼ぶ。 および は通常の非線形システムと同様システムの入力および出力を意味するが、状態と同様に離散的な振舞いを示す可能性がある。 ここで用いられる はすべて について右連続であると仮定する。
式1-1はある特定の離散状態における連続状態の遷移を表わしたものであり、通常の非線形システムにおける状態方程式に相当する。 同様に、式1-4はシステムの出力方程式である。 式1-2および1-3はハイブリッドシステムとしての挙動を記述するためのものであり、それぞれ離散状態の遷移(離散遷移 (discrete transition) やスイッチ (switch) と呼ばれる)と連続状態の不連続な遷移(ジャンプ (jump) と呼ばれる)を規定する。ここで は左極限値 を意味する。 スイッチとジャンプはハイブリッドシステムにみられる特有の状態遷移であり、これらはまとめて事象 (event) と呼ばれる。 事象の生起ルールは、おおまかに次の2種類に大別される。
- 自律スイッチ/自律ジャンプ (autonomous switch/jump) - システムの(ハイブリッド)状態がある条件を満たすことによって生じる事象。
- 制御スイッチ/制御ジャンプ (controlled switch/jump) - 外部入力によって強制的に生起される事象。
具体的なシステムモデル
上のように記述されるモデルは一般的なハイブリッドシステムを記述することが出来る。 一方、対象となるシステムのダイナミクスを詳細に表わしたり理論的な分析や制御器の設計に関する議論をしやすくするなどの理由から、以下に挙げるようなハイブリッドシステムのモデルが提案されている。
ハイブリッドオートマトン
ハイブリッドオートマトン (hybrid automaton) は、有限オートマトンの状態ノードを離散状態に、およびノード間の遷移を事象の生起に対応させることで記述されるシステムモデルである。 (通常の)有限オートマトンと異なり、ハイブリッドオートマトンでは現在のモードの値に加えて連続状態や制御入力の値を考慮してモードの遷移条件(あるいは不変条件)が定められる。 この遷移条件のことをガード (guard)、不変条件をインヴァリアント (invariant) と呼ぶ。
区分的アファインシステムモデル
区分的アファインシステムモデル (piecewise affine system model; PWA model) は、システムの状態方程式が区分アファインな関数として与えられるシステムモデルである。 具体的には、状態 と入力 の組がある部分集合 にあるときの状態方程式が であるように与えられる。 特に が状態空間と制御入力の集合の積集合である の分割であれば各 に対応する が一意に定まり、このときの をモードとみなすことで一般的なハイブリッドシステムの形式へと帰着することが出来る。 すべての において である場合は区分的線形システムモデル (piecewise linear model; PWL model) と呼ばれる。
線形相補性システムモデル
線形相補性システムモデル (linear complementary system model; LC system model) は、相補性条件 (complementary condition) を用いてシステムの離散状態を表現するモデルである。 一般的な LC システムモデルは次のように与えられる。
ここで、 は相補性条件を記述するための補助変数であり、相補性変数 (complementary variable) と呼ばれる。 各成分に対する制約 から、相補性条件は がすべての で成り立つことと等価であり、これは と のいずれか(または両方)が必ずゼロでなければいけないことを意味している。
混合論理動的システムモデル
混合論理動的システムモデル (mixed-logical dynamical system model; MLD system model) は、システムの挙動に関する命題論理を等価な不等式制約で記述することで得られるシステムモデルである。 一般的な MLD システムモデルは、次のように記述される。 ここで および は補助変数 (auxiliary variable) であり、特に はこのシステムモデルにおける離散状態に対応する。
スイッチドシステムモデル
スイッチドシステムモデル (switched system model) は、外部からの離散信号によってシステムのダイナミクスが切り替わるような挙動を表現するためのハイブリッドシステムモデルである。 典型的なスイッチドシステムは次のように記述される。
ここで はスイッチ信号 (switching signal) と呼ばれ、システムの外部から入力される離散的な入力を意味する。
その他のモデル
上に挙げたシステムモデルの他にも、ハイブリッドシステムを扱うためのモデルがいくつか提案されている:
- max-plus 代数システムモデル (max-plus discrete event system model) - 線形演算(和とスカラー倍)に 演算を加えた代数操作のみで状態方程式・出力方程式を記述するシステムモデル
- ハイブリッドペトリネット (hybrid Petri net) - 離散事象システムを記述する数理モデルであるペトリネットを連続状態を扱えるよう拡張したもの
- 確率的ハイブリッドシステムモデル (stochastic hybrid system model)
ハイブリッドシステムの例
物体の衝突
2つの球が地面を転がっている状況を考える(簡単のため、地面との摩擦はないと仮定し、一方向の運動のみを考える)。 2つの球の質量は等しいものとし、水平方向の位置および速度をそれぞれ と表記する。 球の初期位置は を満たし、さらに衝突の前後で球1が球2を追い越すことはない、すなわち任意の時刻で であると仮定する。 このとき、各球の運動は の値によって次のように場合分けされる。
- のとき、それぞれの球の運動は干渉しないので、等速直線運動 によって各球の状態が決定される。
- のとき、2つの球は衝突し速度が不連続に変化する。このときの速度は、運動量保存則と力学的エネルギー保存則を満たし、さらに追い越しに関する上記の制約から次のように与えられる。
すなわち、 および が成立した時点で自律ジャンプが生起される。 ここで をシステムの連続状態とすれば、ハイブリッドシステムとしての状態遷移およびジャンプは次のように記述することが出来る。
解の特異性
ハイブリッドシステムは離散事象システムを内包しているため、解の挙動は通常の(連続なベクトル場を持つ)システムでは見られない特異性を持つことがある。 特に対象とするシステムを分析するにあたって、状態方程式における解の一意性だけでは不十分であり、事象の発生にともないシステムの解が次のような挙動を示すのかどうかを確認し、好ましくない事象が生起しないことを保証するための前提条件を見定める必要がある。
- 事象の生起時刻において、遷移先のモードが存在しないことを デッドロック (deadlock)、複数の遷移先モードの値が存在し一意に定まらないことを 複数解 (multiple solutions) と言う。モデル上で遷移先のモードが指定されていた場合でも、遷移した時点からの連続状態の解が存在しなければ、そのモード遷移は実質的に無効であることに注意する。反対に、モデル上で複数個の遷移先モードが指定されていた場合においても、連続状態の解が存在しないモードを除くことで遷移先のモードが一意に定まることがある。
- ある時刻において事象が生起した後、時刻が進むことなく複数の事象が立て続けに生起することを複数事象 (multiple events) と言う。例えば、ある時点において自律ジャンプが生起することで連続状態の値が変化した後、その状態の値が別の自律スイッチの遷移条件を満たすことによってモード遷移が発生することがある。特に生起する事象が可算個存在し、事象がすべて生起し終えた後の状態の値が定まらない(すなわち、 番目の事象が生起した時点における状態を と表記したとき極限 または のいずれかが存在しない)現象はライブロック (livelock) と呼ばれる。
- ある解における事象の生起時刻 ( を満たす)が有限な集積点 を持つとき、その解は ゼノン解 (Zeno solution) と呼ばれる。例えば地面と衝突し跳躍するボールの運動を考えたとき、地面との弾性係数が 1 よりも小さければ衝突後の最高到達地点は次第に小さくなり、ある時刻でボールの水平運動は完全に停止する。
スライディングモード
次のような離散時間不連続システムを考える(ただし は定数ベクトルである)。 いま および が成り立つと仮定する。 このとき、システムの解は超平面 に吸い込まれるように発展し、十分時間が経過した後における解の挙動は 付近で振動するようなものとなる。 ここでサンプリング周期の極限 を考えると、 解はあたかもモードの境界面である 上で発展しているとみなせる。 このような解の挙動をスライディング動作 (sliding motion) と言う。
上のシステムを連続時間で表わすと、次のようになる。 ただし は を満たす定数であり、一意に定まる。 ここで追加された超平面 上で発展する挙動は、元々存在していたモード( および )のいずれとも異なる新たに生成されたモードであり、スライディングモード (sliding mode) と呼ばれる。
関連する話題
区分的アファインシステムの同定
区分的アファインシステムの同定手法として、時系列データの統計モデルであるARX モデルに離散状態を追加した piecewise ARX (PWARX) モデルへのアプローチが提案されている。
混合論理動的システムの制御
混合論理動的システムの制御手法として、有限時間最適制御問題を実時間で逐次的に解くことで制御入力を決定するモデル予測制御 (en:英語版) を用いた手法が広く知られている。 特に離散時間 MLD システムでは、解くべき最適化問題は混合整数計画問題 (mixed integer programming problem; MIP -) に帰着する。 これは組合せ最適化の一種であり、一般にNP困難であることが知られている。
出典
参考文献
- 井村順一; 東俊一; 増淵泉『ハイブリッドシステムの制御』コロナ社、2014年1月6日。ISBN 978-4-339-03320-5。
- 川嶋宏彰、松山隆司「ハイブリッドダイナミカルシステムによる動的事象のモデル化と認識(<特集>ダイナミクスに基づく情報処理の諸相)」『システム/制御/情報』第54巻第1号、システム制御情報学会、2010年、28-33頁、doi:10.11509/isciesci.54.1_28。
- 鷹羽浄嗣、仲田勇人「区分的アフィンシステムの同定(<特集>「動的システムのモデリングの新展開」)」『システム/制御/情報』第50巻第3号、システム制御情報学会、2006年、87-92頁、doi:10.11509/isciesci.50.3_87。
- H. Witsenhausen (1966). “A class of hybrid-state continuous-time dynamic systems”. IEEE Transactions on Automatic Control 11 (2): 161-167. doi:10.1109/TAC.1966.1098336.
- Bemporad, Alberto; Morari, Manfred (1999), “Control of systems integrating logic, dynamics, and constraints”, Automatica 35 (3): 407-427, doi:10.1016/S0005-1098(98)00178-2
- B. De Schutter; T. J. J. van den Boom (2002), Model predictive control for max-min-plus-scaling systems - efficient implementation, Zaragoza, Spain, doi:10.1109/WODES.2002.1167709
- Jun Zhang; Karl Henrik Johansson; John Lygeros; Shankar Sastry (2001-04-30), “Zeno hybrid systems”, International Journal of Robust and Nonlinear Control 11 (5): 435-451, doi:10.1002/rnc.592
関連項目
- 制御理論
- 離散事象システム
- 非線形システム論
- オートマトン
- グラフ理論
- 計算複雑性理論
- 計算機科学
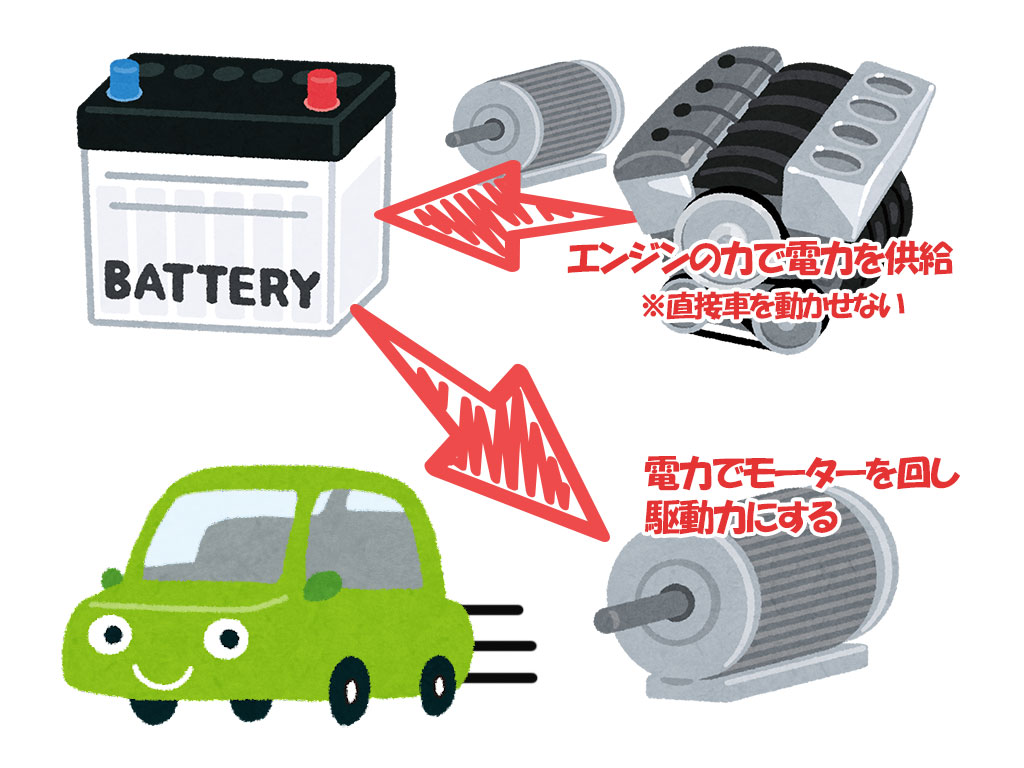

![トヨタのTHSをどう縦置きボクサーに載せた? スバルXVの2モーター式ハイブリッドシステムとTHS|MotorFanTECH[モーターファンテック]](https://car.motor-fan.jp/images/articles/10006619/big_main10006619_20181122125557000000.jpg)